publications | Chris Howland

2025

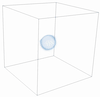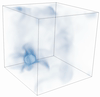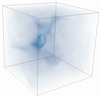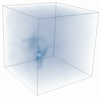A front-tracking immersed-boundary framework for simulating Lagrangian melting problems

Kevin Zhong, Christopher J. Howland, Detlef Lohse, and 1 more author

J. Comput. Phys., Mar 2025

Abs DOI Bib

In so-called Lagrangian melting problems, a solid immersed in a fluid medium is free to rotate and translate in tandem with its phase-change from solid to liquid. Such configurations may be classified as a fluid-solid interaction (FSI) problem coupled to phase-change. Our present work proposes a numerical method capable of simulating these Lagrangian melting problems and adopts a front-tracking immersed-boundary (IB) method. We use the moving least squares IB framework, a well-established method for simulating a diverse range of FSI problems and extend this framework to accommodate melting by additionally imposing the Stefan condition at the interface. In the spirit of canonical front-tracking methods, the immersed solid is represented by a discrete triangulated mesh which is separate from the Eulerian mesh in which the governing flow equations are solved. A known requirement for these methods is the need for comparable Eulerian and Lagrangian grid spacings to stabilise interpolation and spreading operations between the two grids. For a melting object, this requirement is inevitably violated unless interventional remeshing is introduced. Our work therefore presents a novel dynamic remeshing procedure to overcome this. The remeshing is based on a gradual coarsening of the triangulated Lagrangian mesh and amounts to a negligible computational burden per timestep owing to the incremental and local nature of its operations, making it a scalable approach. Moreover, the coarsening is coupled to a volume-conserving smoothing procedure detailed by Kuprat et al., ensuring a zero net volume change in the remeshing step to machine precision. This added feature makes our present method highly specialised to the study of melting problems, where precise measurements of the melting solid’s volume is often the primary predictive quantity of interest.
@article{zhong_front-tracking_2025, title = {A front-tracking immersed-boundary framework for simulating {Lagrangian} melting problems}, volume = {525}, doi = {10.1016/j.jcp.2025.113762}, journal = {J. Comput. Phys.}, author = {Zhong, Kevin and Howland, Christopher J. and Lohse, Detlef and Verzicco, Roberto}, month = mar, year = {2025}, keywords = {Eulerian–Lagrangian, Fluid-solid interaction, Heat transfer, Immersed boundary method, Meshing, Multiphase flow, One-fluid model, Phase change, Stefan problems, Turbulent flows}, pages = {113762}, }

2024

Scaling relations for heat and momentum transport in sheared Rayleigh–Bénard convection

Guru Sreevanshu Yerragolam, Christopher J. Howland, Richard J. A. M. Stevens, and 3 more authors

J. Fluid Mech., Dec 2024

Abs DOI Bib

We provide scaling relations for the Nusselt number \(Nu\)and the friction coefficient \(C_S\)in sheared Rayleigh–Bénard convection, i.e. in Rayleigh–Bénard flow with Couette- or Poiseuille-type shear forcing, by extending the Grossmann & Lohse (J. Fluid Mech., vol. 407, 2000, pp. 27–56, Phys. Rev. Lett., vol. 86, 2001, pp. 3316–3319, Phys. Rev. E, vol. 66, 2002, 016305, Phys. Fluids, vol. 16, 2004, pp. 4462–4472) theory to sheared thermal convection. The control parameters for these systems are the Rayleigh number \(Ra\), the Prandtl number \(Pr\) and the Reynolds number \(Re_S\) that characterises the strength of the imposed shear. By direct numerical simulations and theoretical considerations, we show that, in turbulent Rayleigh–Bénard convection, the friction coefficients associated with the applied shear and the shear generated by the large-scale convection rolls are both well described by Prandtl’s (Ergeb. Aerodyn. Vers. Gött., vol. 4, 1932, pp. 18–29) logarithmic friction law, suggesting some kind of universality between purely shear-driven flows and thermal convection. These scaling relations hold well for \(10^6≤Ra≤10^8\), \(0.5≤Pr≤5.0\), and \(0≤Re_S≤10^4\).
@article{yerragolam_scaling_2024, title = {Scaling relations for heat and momentum transport in sheared {Rayleigh}–{Bénard} convection}, volume = {1000}, doi = {10.1017/jfm.2024.872}, language = {en}, journal = {J. Fluid Mech.}, author = {Yerragolam, Guru Sreevanshu and Howland, Christopher J. and Stevens, Richard J. A. M. and Verzicco, Roberto and Shishkina, Olga and Lohse, Detlef}, month = dec, year = {2024}, keywords = {turbulence simulation, turbulent convection}, pages = {A74}, }
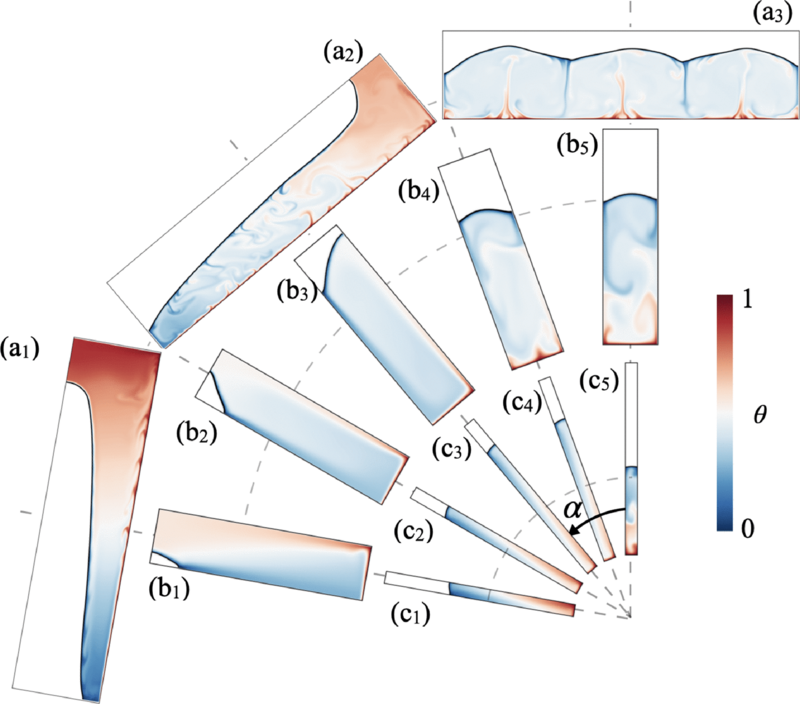Enhanced Efficiency of Latent Heat Energy Storage by Inclination

Rui Yang, Christopher J. Howland, Hao-Ran Liu, and 2 more authors

PRX Energy, Nov 2024

Abs DOI Bib

Latent heat storage (LHS) has emerged as a promising solution for addressing the challenges of large-scale and long-term energy storage, offering a clean and reusable system. Being in the developmental stage, and with only limited theoretical predictions being available, there is a need to enhance the efficiency of LHS systems. In this study, we use numerical simulations to study the melting process of a phase-change material (PCM) in a rectangular domain. A significant enhancement in the melt rate of the PCM is found by a simple inclination of the domain, with a 60% increase in melt rate compared to a standard square unit without inclination through enhanced heat transfer. We establish a theoretical relation for the optimal PCM melt rate, based on the inclination angle and the domain aspect ratio, outlining the optimal conditions for the PCM melt rate, which is solely dependent on the domain geometry. We further propose a heat-transfer model that predicts the optimal aspect ratio for achieving the maximum melt rate as a function of the Rayleigh and Prandtl numbers.
@article{yang_enhanced_2024, title = {Enhanced {Efficiency} of {Latent} {Heat} {Energy} {Storage} by {Inclination}}, volume = {3}, doi = {10.1103/PRXEnergy.3.043006}, number = {4}, journal = {PRX Energy}, author = {Yang, Rui and Howland, Christopher J. and Liu, Hao-Ran and Verzicco, Roberto and Lohse, Detlef}, month = nov, year = {2024}, pages = {043006}, }
Turbulent mixed convection in vertical and horizontal channels

Christopher J. Howland, Guru Sreevanshu Yerragolam, Roberto Verzicco, and 1 more author

J. Fluid Mech., Nov 2024

Abs DOI Bib

Turbulent shear flows driven by a combination of a pressure gradient and buoyancy forcing are investigated using direct numerical simulations. Specifically, we consider the set-up of a differentially heated vertical channel subject to a Poiseuille-like horizontal pressure gradient. We explore the response of the system to its three control parameters: the Grashof number \(Gr\), the Prandtl number \(Pr\), and the Reynolds number \(Re\)of the pressure-driven flow. From these input parameters, the relative strength of buoyancy driving to the pressure gradient can be quantified by the Richardson number \(Ri=Gr/Re^2\). We compare the response of the mixed vertical convection configuration to that of mixed Rayleigh–Bénard convection, and find a nearly identical behaviour, including an increase in wall friction at higher \(Gr\), and a drop in the heat flux relative to natural convection for \(Ri=O(1)\). This closely matched response is despite vastly different flow structures in the systems. No large-scale organisation is visible in visualisations of mixed vertical convection – an observation that is confirmed quantitatively by spectral analysis. This analysis, combined with a statistical description of the wall heat flux, highlights how moderate shear suppresses the growth of small-scale plumes and reduces the likelihood of extreme events in the local wall heat flux. Vice versa, starting from a pure shear flow, the addition of thermal driving enhances the drag due to the emission of thermal plumes.
@article{howland_turbulent_2024, title = {Turbulent mixed convection in vertical and horizontal channels}, volume = {998}, doi = {10.1017/jfm.2024.598}, language = {en}, journal = {J. Fluid Mech.}, author = {Howland, Christopher J. and Yerragolam, Guru Sreevanshu and Verzicco, Roberto and Lohse, Detlef}, month = nov, year = {2024}, keywords = {buoyant boundary layers, turbulent boundary layers, turbulent convection}, pages = {A48}, }
Effect of airflow rate on CO2 concentration in downflow indoor ventilation

Guru Sreevanshu Yerragolam, Christopher J. Howland, Rui Yang, and 3 more authors

Indoor Environments, Jun 2024

Abs DOI Bib

We perform direct numerical simulations to study the effect of increasing airflow rate on CO2 concentration in downflow and displacement ventilation in a room with one occupant. Often, CO2 concentration is used as a proxy for the concentration of bio-aerosols of respiratory droplets, and therefore, tracking the CO2 concentration in ventilation strategies can be useful to understand and quantify the risk of spread of communicable respiratory illnesses. At low to moderate airflow rates, the flow in the downflow setup is not mixed, but stratified. The CO2 concentration in the upper and lower layers is determined by the strength of the thermal plume originating from the occupant. We provide a simple theoretical model to predict the height of the stratified interface, the volumetric flux of the ascending plume, and the CO2 concentration in the lower and upper layers. At very high airflow rates, the flow is well-mixed and the average CO2 concentration in the room can be predicted with the mixing ventilation assumption. We demonstrate that at low to moderate airflow rates, displacement ventilation more effectively maintains lower CO2 concentrations in the lower layer compared to downflow ventilation.
@article{yerragolam_effect_2024, title = {Effect of airflow rate on {CO2} concentration in downflow indoor ventilation}, volume = {1}, url = {https://www.sciencedirect.com/science/article/pii/S2950362024000092}, doi = {10.1016/j.indenv.2024.100012}, number = {2}, journal = {Indoor Environments}, author = {Yerragolam, Guru Sreevanshu and Howland, Christopher J. and Yang, Rui and Stevens, Richard J. A. M. and Verzicco, Roberto and Lohse, Detlef}, month = jun, year = {2024}, keywords = {Direct numerical simulations, Thermal convection, Transport, Turbulence, Ventilation}, pages = {100012}, }
Towards the understanding of convective dissolution in confined porous media: thin bead pack experiments, two-dimensional direct numerical simulations and physical models

Marco De Paoli, Christopher J. Howland, Roberto Verzicco, and 1 more author

J. Fluid Mech., May 2024

Abs DOI Bib

We consider the process of convective dissolution in a homogeneous and isotropic porous medium. The flow is unstable due to the presence of a solute that induces a density difference responsible for driving the flow. The mixing dynamics is thus driven by a Rayleigh–Taylor instability at the pore scale. We investigate the flow at the scale of the pores using Hele-Shaw type experiment with bead packs, two-dimensional direct numerical simulations and physical models. Experiments and simulations have been specifically designed to mimic the same flow conditions, namely matching porosities, high Schmidt numbers and linear dependency of fluid density with solute concentration. In addition, the solid obstacles of the medium are impermeable to fluid and solute. We characterise the evolution of the flow via the mixing length, which quantifies the extension of the mixing region and grows linearly in time. The flow structure, analysed via the centreline mean wavelength, is observed to grow in agreement with theoretical predictions. Finally, we analyse the dissolution dynamics of the system, quantified through the mean scalar dissipation, and three mixing regimes are observed. Initially, the evolution is controlled by diffusion, which produces solute mixing across the initial horizontal interface. Then, when the interfacial diffusive layer is sufficiently thick, it becomes unstable, forming finger-like structures and driving the system into a convection-dominated phase. Finally, when the fingers have grown sufficiently to touch the horizontal boundaries of the domain, the mixing reduces dramatically due to the absence of fresh unmixed fluid. With the aid of simple physical models, we explain the physics of the results obtained numerically and experimentally. The solute evolution presents a self-similar behaviour, and it is controlled by different length scales in each stage of the mixing process, namely the length scale of diffusion, the pore size and the domain height.
@article{de_paoli_towards_2024, title = {Towards the understanding of convective dissolution in confined porous media: thin bead pack experiments, two-dimensional direct numerical simulations and physical models}, volume = {987}, doi = {10.1017/jfm.2024.328}, language = {en}, journal = {J. Fluid Mech.}, author = {De Paoli, Marco and Howland, Christopher J. and Verzicco, Roberto and Lohse, Detlef}, month = may, year = {2024}, keywords = {porous media, convection in porous media, dispersion}, pages = {A1}, }
Shape effect on solid melting in flowing liquid

Rui Yang, Christopher J. Howland, Hao-Ran Liu, and 2 more authors

J. Fluid Mech., Feb 2024

Abs DOI Bib

Iceberg melting is a critical factor for climate change. However, the shape of an iceberg is an often neglected aspect of its melting process. Our study investigates the influence of different ice shapes and ambient flow velocities on melt rates by conducting direct numerical simulations of a simplified system of bluff body flow. Our study focuses on the ellipsoidal shape, with the aspect ratio as the control parameter. We found the shape plays a crucial role in the melting process, resulting in significant variations in the melt rate between different shapes. Without flow, the optimal shape for a minimal melt rate is the disk (two-dimensional) or sphere (three-dimensional), due to the minimal surface area. However, as the ambient flow velocity increases, the optimal shape changes with the aspect ratio. We find that ice with an elliptical shape (when the long axis is aligned with the flow direction) can melt up to 10% slower than a circular shape when exposed to flowing water. Following the approach considered by Huang et al. (J. Fluid Mech., vol. 765, 2015, R3) for dissolving bodies, we provide a quantitative theoretical explanation for this optimal shape, based on the combined contributions from both surface-area effects and convective-heat-transfer effects. Our findings provide insight into the interplay between phase transitions and ambient flows, contributing to our understanding of the iceberg melting process and highlighting the need to consider the aspect-ratio effect in estimates of iceberg melt rates.
@article{yang_shape_2024, title = {Shape effect on solid melting in flowing liquid}, author = {Yang, Rui and Howland, Christopher J. and Liu, Hao-Ran and Verzicco, Roberto and Lohse, Detlef}, year = {2024}, month = feb, journal = {J. Fluid Mech.}, volume = {980}, pages = {R1}, publisher = {{Cambridge University Press}}, doi = {10.1017/jfm.2023.1080}, keywords = {sea ice,solidification/melting}, }

2023

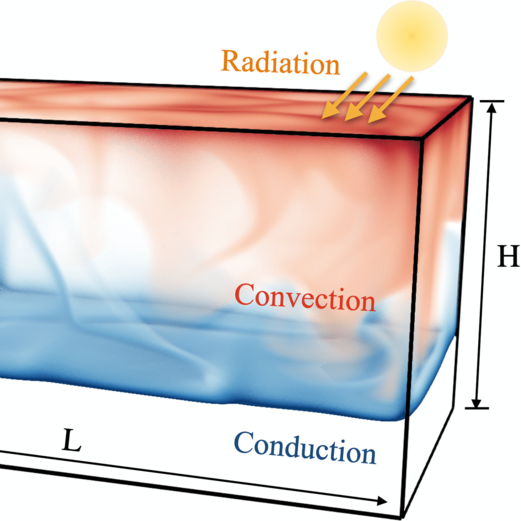Bistability in Radiatively Heated Melt Ponds

Rui Yang, Christopher J. Howland, Hao-Ran Liu, and 2 more authors

Phys. Rev. Lett., Dec 2023

Abs DOI Bib

Melting and solidification processes, intertwined with convective flows, play a fundamental role in geophysical contexts. One of these processes is the formation of melt ponds on glaciers, ice shelves, and sea ice. It is driven by solar radiation and is of great significance for Earth’s heat balance, as it significantly lowers the albedo. Through direct numerical simulations and theoretical analysis, we unveil a bistability phenomenon in the melt pond dynamics. As solar radiation intensity and the melt pond’s initial depth vary, an abrupt transition occurs: this tipping point transforms the system from a stable fully frozen state to another stable equilibrium state, characterized by a distinct melt pond depth. The physics of this transition can be understood within a heat flux balance model, which exhibits excellent agreement with our numerical results. Together with the Grossmann-Lohse theory for internally heated convection, the model correctly predicts the bulk temperature and the flow strength within the melt ponds, offering insight into the coupling of phase transitions with adjacent turbulent flows and the interplay between convective melting and radiation-driven processes.
@article{yang_bistability_2023, title = {Bistability in {{Radiatively Heated Melt Ponds}}}, author = {Yang, Rui and Howland, Christopher J. and Liu, Hao-Ran and Verzicco, Roberto and Lohse, Detlef}, year = {2023}, month = dec, journal = {Phys. Rev. Lett.}, volume = {131}, number = {23}, pages = {234002}, doi = {10.1103/PhysRevLett.131.234002}, }
Ice melting in salty water: layering and non-monotonic dependence on the mean salinity

Rui Yang, Christopher J. Howland, Hao-Ran Liu, and 2 more authors

J. Fluid Mech., Aug 2023

Abs DOI Bib

The presence of salt in seawater strongly affects the melt rate and the shape evolution of ice, both of utmost relevance in ice–ocean interactions and thus for the climate. To get a better quantitative understanding of the physical mechanics at play in ice melting in salty water, we numerically investigate the lateral melting of an ice block in stably stratified saline water. The developing ice shape from our numerical results shows good agreement with the experiments and theory from Huppert & Turner (J. Fluid Mech., vol. 100, 1980, pp. 367–384). Furthermore, we find that the melt rate of ice depends non-monotonically on the mean ambient salinity: it first decreases for increasing salt concentration until a local minimum is attained, and then increases again. This non-monotonic behaviour of the ice melt rate is due to the competition among salinity-driven buoyancy, temperature-driven buoyancy and salinity-induced stratification. We develop a theoretical model based on the force balance which gives a prediction of the salt concentration for which the melt rate is minimal, and is consistent with our data. Our findings give insight into the interplay between phase transitions and double-diffusive convective flows.
@article{yang_ice_2023, title = {Ice melting in salty water: layering and non-monotonic dependence on the mean salinity}, shorttitle = {Ice Melting in Salty Water}, author = {Yang, Rui and Howland, Christopher J. and Liu, Hao-Ran and Verzicco, Roberto and Lohse, Detlef}, year = {2023}, month = aug, journal = {J. Fluid Mech.}, volume = {969}, pages = {R2}, doi = {10.1017/jfm.2023.582}, keywords = {Bénard convection,double diffusive convection}, }
Morphology evolution of a melting solid layer above its melt heated from below

Rui Yang, Christopher J. Howland, Hao-Ran Liu, and 2 more authors

J. Fluid Mech., Feb 2023

Abs DOI Bib

We numerically study the melting process of a solid layer heated from below such that a liquid melt layer develops underneath. The objective is to quantitatively describe and understand the emerging topography of the structures (characterized by the amplitude and wavelength), which evolve out of an initially smooth surface. By performing both two-dimensional (achieving Rayleigh number up to \(Ra=10^{11}\) and three-dimensional (achieving Rayleigh number up to \(Ra=10^9\)) direct numerical simulations with an advanced finite difference solver coupled to the phase-field method, we show how the interface roughness is spontaneously generated by thermal convection. With increasing height of the melt the convective flow intensifies and eventually even becomes turbulent. As a consequence, the interface becomes rougher but is still coupled to the flow topology. The emerging structure of the interface coincides with the regions of rising hot plumes and descending cold plumes. We find that the roughness amplitude scales with the mean height of the liquid layer. We derive this scaling relation from the Stefan boundary condition and relate it to the non-uniform distribution of heat flux at the interface. For two-dimensional cases, we further quantify the horizontal length scale of the morphology, based on the theoretical upper and lower bounds given for the size of convective cells known from Wang et al. (Phys. Rev. Lett., vol. 125, 2020, 074501). These bounds agree with our simulation results. Our findings highlight the key connection between the morphology of the melting solid and the convective flow structures in the melt beneath.
@article{yang_morphology_2023, title = {Morphology evolution of a melting solid layer above its melt heated from below}, author = {Yang, Rui and Howland, Christopher J. and Liu, Hao-Ran and Verzicco, Roberto and Lohse, Detlef}, year = {2023}, month = feb, journal = {J. Fluid Mech.}, volume = {956}, pages = {A23}, publisher = {{Cambridge University Press}}, doi = {10.1017/jfm.2023.15}, keywords = {Bénard convection,solidification/melting,turbulent convection}, }
Double-diffusive transport in multicomponent vertical convection

Christopher J. Howland, Roberto Verzicco, and Detlef Lohse

Phys. Rev. Fluids, Jan 2023

Abs DOI arXiv Bib

Motivated by the ablation of vertical ice faces in salt water, we use three-dimensional direct numerical simulations to investigate the heat and salt fluxes in two-scalar vertical convection. For parameters relevant to ice-ocean interfaces in the convection-dominated regime, we observe that the salinity field drives the convection and that heat is essentially transported as a passive scalar. By varying the diffusivity ratio of heat and salt (i.e., the Lewis number \(Le\)), we identify how the different molecular diffusivities affect the scalar fluxes through the system. Away from the walls, we find that the heat transport is determined by a turbulent Prandtl number of \(Pr_t ≈1\) and that double-diffusive effects are practically negligible. However, the difference in molecular diffusivities plays an important role close to the boundaries. In the (unrealistic) case where salt diffused faster than heat, the ratio of salt-to-heat fluxes would scale as \(Le^{1/3}\), consistent with classical nested scalar boundary layers. However, in the realistic case of faster heat diffusion (relative to salt), we observe a transition towards a \(Le^{1/2}\) scaling of the ratio of the fluxes. This coincides with the thermal boundary layer width growing beyond the thickness of the viscous boundary layer. We find that this transition is not determined by a critical Lewis number, but rather by a critical Prandtl number \(Pr ≈10\), slightly below that for cold seawater where \(Pr=14\). We compare our results to similar studies of sheared and double-diffusive flow under ice shelves, and discuss the implications for fluxes in large-scale ice-ocean models. By coupling our results to ice-ocean interface thermodynamics, we describe how the flux ratio impacts the interfacial salinity, and hence the strength of solutal convection and the ablation rate.
@article{howland_double-diffusive_2023, title = {Double-diffusive transport in multicomponent vertical convection}, author = {Howland, Christopher J. and Verzicco, Roberto and Lohse, Detlef}, year = {2023}, month = jan, journal = {Phys. Rev. Fluids}, volume = {8}, number = {1}, pages = {013501}, publisher = {{American Physical Society}}, doi = {10.1103/PhysRevFluids.8.013501}, }

2022

Boundary layers in turbulent vertical convection at high Prandtl number

Christopher J. Howland, Chong Shen Ng, Roberto Verzicco, and 1 more author

J. Fluid Mech., Jan 2022

Abs DOI arXiv Bib

Many environmental flows arise due to natural convection at a vertical surface, from flows in buildings to dissolving ice faces at marine-terminating glaciers. We use three-dimensional direct numerical simulations of a vertical channel with differentially heated walls to investigate such convective, turbulent boundary layers. Through the implementation of a multiple-resolution technique, we are able to perform simulations at a wide range of Prandtl numbers \(Pr\). This allows us to distinguish the parameter dependences of the horizontal heat flux and the boundary layer widths in terms of the Rayleigh number \(Ra\) and Prandtl number \(Pr\). For the considered parameter range \(1≤Pr≤100\), \(10^6≤Ra≤10^9\), we find the flow to be consistent with a ’buoyancy-controlled’ regime where the heat flux is independent of the wall separation. For given \(Pr\), the heat flux is found to scale linearly with the friction velocity \(V_∗\). Finally, we discuss the implications of our results for the parameterisation of heat and salt fluxes at vertical ice-ocean interfaces.
@article{howland_boundary_2022, title = {Boundary layers in turbulent vertical convection at high {{Prandtl}} number}, author = {Howland, Christopher J. and Ng, Chong Shen and Verzicco, Roberto and Lohse, Detlef}, year = {2022}, month = jan, journal = {J. Fluid Mech.}, volume = {930}, pages = {A32}, publisher = {{Cambridge University Press}}, doi = {10.1017/jfm.2021.952}, keywords = {buoyant boundary layers,turbulent boundary layers,turbulent convection}, }

2021

Optimal Perturbation Growth on a Breaking Internal Gravity Wave

J. P. Parker, C. J. Howland, C. P. Caulfield, and 1 more author

J. Fluid Mech., Oct 2021

Abs DOI Bib

The breaking of internal gravity waves in the abyssal ocean is thought to be responsible for much of the mixing necessary to close oceanic buoyancy budgets. The exact mechanism by which these waves break down into turbulence remains an active area of research and can have significant implications on the mixing efficiency. Recent evidence has suggested that both shear instabilities and convective instabilities play a significant role in the breaking of an internal gravity wave in a high Richardson number mean shear flow. We perform a systematic analysis of the stability of a configuration of an internal gravity wave superimposed on a background shear flow first considered by Howland et al. (J. Fluid Mech., vol. 921, 2021, A24), using direct-adjoint looping to find the perturbation giving maximal energy growth on this evolving flow. We find that three-dimensional, convective mechanisms produce greater energy growth than their two-dimensional counterparts. In particular, we find close agreement with the direct numerical simulations of Howland et al. (J. Fluid Mech., vol. 921, 2021, A24), which demonstrated a clear three-dimensional mechanism causing breakdown to turbulence. The results are shown to hold at realistic Prandtl numbers. At low mean Richardson numbers, two-dimensional, shear-driven mechanisms produce greater energy growth.
@article{parker_optimal_2021, title = {Optimal Perturbation Growth on a Breaking Internal Gravity Wave}, author = {Parker, J. P. and Howland, C. J. and Caulfield, C. P. and Kerswell, R. R.}, year = {2021}, month = oct, journal = {J. Fluid Mech.}, volume = {925}, publisher = {{Cambridge University Press}}, doi = {10.1017/jfm.2021.603}, copyright = {All rights reserved}, langid = {english}, keywords = {shear-flow instability,stratified flows}, }
Shear-Induced Breaking of Internal Gravity Waves

Christopher J. Howland, John R. Taylor, and C. P. Caulfield

J. Fluid Mech., Aug 2021

Abs DOI arXiv Bib

Motivated by observations of turbulence in the strongly stratified ocean thermocline, we use direct numerical simulations to investigate the interaction of a sinusoidal shear flow and a large-amplitude internal gravity wave. Despite strong nonlinearities in the flow and a lack of scale separation, we find that linear ray-tracing theory is qualitatively useful in describing the early development of the flow as the wave is refracted by the shear. Consistent with the linear theory, the energy of the wave accumulates in regions of negative mean shear where we observe evidence of convective and shear instabilities. Streamwise-aligned convective rolls emerge the fastest, but their contribution to irreversible mixing is dwarfed by shear-driven billow structures that develop later. Although the wave strongly distorts the buoyancy field on which these billows develop, the mixing efficiency of the subsequent turbulence is similar to that arising from Kelvin-Helmholtz instability in a stratified shear layer. We run simulations at Reynolds numbers \(Re\) of 5000 and 8000, and vary the initial amplitude of the internal gravity wave. For high values of initial wave amplitude, the results are qualitatively independent of \(Re\). Smaller initial wave amplitudes delay the onset of the instabilities, and allow for significant laminar diffusion of the internal wave, leading to reduced turbulent activity. We discuss the complex interaction between the mean flow, internal gravity wave and turbulence, and its implications for internal wave-driven mixing in the ocean.
@article{howland_shear-induced_2021, title = {Shear-Induced Breaking of Internal Gravity Waves}, author = {Howland, Christopher J. and Taylor, John R. and Caulfield, C. P.}, year = {2021}, month = aug, journal = {J. Fluid Mech.}, volume = {921}, pages = {A24}, publisher = {{Cambridge University Press}}, issn = {0022-1120, 1469-7645}, doi = {10.1017/jfm.2021.506}, copyright = {All rights reserved}, langid = {english}, keywords = {internal waves,stratified turbulence,wave breaking}, }
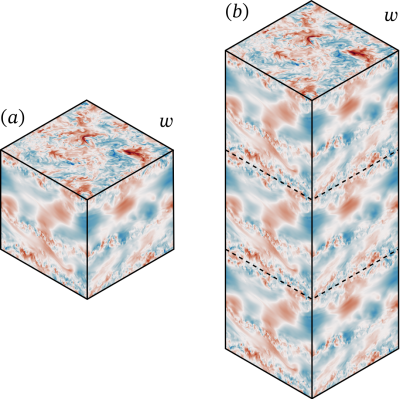Quantifying Mixing and Available Potential Energy in Vertically Periodic Simulations of Stratified Flows

Christopher J. Howland, John R. Taylor, and C. P. Caulfield

J. Fluid Mech., May 2021

Abs DOI arXiv Bib

Turbulent mixing exerts a significant influence on many physical processes in the ocean. In a stably stratified Boussinesq fluid, this irreversible mixing describes the conversion of available potential energy (APE) to background potential energy (BPE). In some settings the APE framework is difficult to apply and approximate measures are used to estimate irreversible mixing. For example, numerical simulations of stratified turbulence often use triply periodic domains to increase computational efficiency. In this set-up, however, BPE is not uniquely defined and the method of Winters et al. (J. Fluid Mech., vol. 289, 1995, pp. 115-128) cannot be directly applied to calculate the APE. We propose a new technique to calculate APE in periodic domains with a mean stratification. By defining a control volume bounded by surfaces of constant buoyancy, we can construct an appropriate background buoyancy profile \(b_∗(z,t)\) and accurately quantify diapycnal mixing in such systems. This technique also permits the accurate calculation of a finite-amplitude local APE density in periodic domains. The evolution of APE is analysed in various turbulent stratified flow simulations. We show that the mean dissipation rate of buoyancy variance \(χ\) provides a good approximation to the mean diapycnal mixing rate, even in flows with significant variations in local stratification. When quantifying measures of mixing efficiency in transient flows, we find significant variation depending on whether laminar diffusion of a mean flow is included in the kinetic energy dissipation rate. We discuss how best to interpret these results in the context of quantifying diapycnal diffusivity in real oceanographic flows.
@article{howland_quantifying_2021, title = {Quantifying Mixing and Available Potential Energy in Vertically Periodic Simulations of Stratified Flows}, author = {Howland, Christopher J. and Taylor, John R. and Caulfield, C. P.}, year = {2021}, month = may, journal = {J. Fluid Mech.}, volume = {914}, pages = {A12}, publisher = {{Cambridge University Press}}, issn = {0022-1120, 1469-7645}, doi = {10.1017/jfm.2020.979}, copyright = {All rights reserved}, langid = {english}, keywords = {ocean processes,stratified turbulence}, }

2020

Mixing in Forced Stratified Turbulence and Its Dependence on Large-Scale Forcing

Christopher J. Howland, John R. Taylor, and C. P. Caulfield

J. Fluid Mech., Sep 2020

Abs DOI Bib

We study direct numerical simulations of turbulence arising from the interaction of an initial background shear, a linear background stratification and an external body force. In each simulation the turbulence produced is spatially intermittent, with dissipation rates varying over orders of magnitude in the vertical. We focus analysis on the statistically quasi-steady states achieved by applying large-scale body forcing to the domain, and compare flows forced by internal gravity waves with those forced by vertically uniform vortical modes. By considering the turbulent energy budgets for each simulation, we find that the injection of potential energy from the wave forcing permits a reversal in the sign of the mean buoyancy flux. This change in the sign of the buoyancy flux is associated with large, convective density overturnings, which in turn lead to more efficient mixing in the wave-forced simulations. The inhomogeneous dissipation in each simulation allows us to investigate localised correlations between the kinetic and potential energy dissipation rates. These correlations lead us to the conclusion that an appropriate definition of an instantaneous mixing efficiency, \(η(t):=χ/(χ+ \varepsilon)\) (where \(\varepsilon\) and \(χ\) are the volume-averaged turbulent viscous dissipation rate and fluctuation density variance destruction rate respectively) in the wave-forced cases is independent of an appropriately defined local turbulent Froude number, consistent with scalings proposed for low Froude number stratified turbulence.
@article{howland_mixing_2020, title = {Mixing in Forced Stratified Turbulence and Its Dependence on Large-Scale Forcing}, author = {Howland, Christopher J. and Taylor, John R. and Caulfield, C. P.}, year = {2020}, month = sep, journal = {J. Fluid Mech.}, volume = {898}, pages = {A7}, publisher = {{Cambridge University Press}}, issn = {0022-1120, 1469-7645}, doi = {10.1017/jfm.2020.383}, langid = {english}, keywords = {stratified flows,stratified turbulence,turbulent mixing}, }
Energetics and Mixing in Stratified Turbulent Flows

Christopher James Howland

Nov 2020

Abs DOI Bib

Turbulent mixing has an important influence on many physical processes in the ocean. For example, the upwelling of water through the stably stratified ocean interior, needed to close the global circulation, is only possible through the enhanced vertical mixing resulting from turbulence. The transport of heat, carbon and nutrients is also affected by this mixing. Understanding its spatial and temporal intermittency is therefore vital for determining the regional distribution of these important tracers. Away from boundaries, turbulence in the ocean is commonly attributed to the breaking of internal waves. When an internal wave grows to a large amplitude, it can break due to convective instabilities or shear instabilities. A fundamental understanding of the turbulent transition arising from these instabilities is useful for both interpreting observations and predicting ’hotspots’ of turbulence in the field. Focusing solely on canonical instabilities however neglects the wide range of complex flows occurring at small scales in the ocean. Interactions with mean flows or with the background internal wave field can alter the properties of turbulence and the ensuing mixing. In this thesis, we use numerical simulations to investigate three problems aimed at enhancing our understanding of mixing in such stratified flows. We first investigate the development of Kelvin-Helmholtz instability in a stratified shear layer. We quantify the maximum energy extracted from the mean flow by the instability as a function of the Richardson number \(Ri\). By applying forcing to the governing equations, we are able to extend our simulations up to the marginal stability threshold of \(Ri=1/4\), and show that the maximum energy decreases to a small but non-zero value as this threshold is approached. Our next study focuses on mixing in stratified turbulence that is kept in a statistically steady state through large-scale forcing. We compare flows forced by vortical modes with those forced by internal gravity waves. A higher mixing efficiency in the wave-forced simulations is attributed to a more convective-driven mixing process. Intermittency in the flows allows us to verify that the mixing efficiency is constant throughout each domain. This is despite wavelet analysis showing that regions of high and low energy dissipation have distinct scalings in their energy spectra. Finally, we consider the interaction of a large-amplitude internal gravity wave with a sinusoidal shear flow. We find both convective and shear processes to be important in the transition to turbulence. Through extending the concept of available potential energy to triply periodic domains, we show that the scalar variance dissipation rate \(χ\) is a good approximation to the ’true’ rate of mixing \(\mathcal{M}\), even when sizeable regions of static instability are present.
@phdthesis{howland_energetics_2020, type = {Doctoral Thesis}, title = {Energetics and Mixing in Stratified Turbulent Flows}, author = {Howland, Christopher James}, year = {2020}, month = nov, school = {University of Cambridge}, doi = {10.17863/CAM.58686}, }

2018

Testing Linear Marginal Stability in Stratified Shear Layers

C. J. Howland, J. R. Taylor, and C. P. Caulfield

J. Fluid Mech., Mar 2018

Abs DOI Bib

We use two-dimensional direct numerical simulations of Boussinesq stratified shear layers to investigate the influence of the minimum gradient Richardson number \(Ri_m\) on the early time evolution of Kelvin-Helmholtz instability to its saturated ’billow’ state. Even when the diffusion of the background velocity and density distributions is counterbalanced by artificial body forces to maintain the initial profiles, in the limit as \(Ri_m→1/4\), the perturbation growth rate tends to zero and the saturated perturbation energy becomes small. These results imply, at least for such canonical inflectional stratified shear flows, that ’marginally unstable’ flows with \(Ri_m\) only slightly less than 1/4 are highly unlikely to become ’turbulent’, in the specific sense of being associated with significantly enhanced dissipation, irreversible mixing and non-trivial modification of the background distributions without additional externally imposed forcing.
@article{howland_testing_2018, title = {Testing Linear Marginal Stability in Stratified Shear Layers}, author = {Howland, C. J. and Taylor, J. R. and Caulfield, C. P.}, year = {2018}, month = mar, journal = {J. Fluid Mech.}, volume = {839}, pages = {R4}, issn = {0022-1120, 1469-7645}, doi = {10.1017/jfm.2018.79}, langid = {english}, keywords = {geophysical and geological flows,instability,stratified flows}, }

Turbulent Point Source Plumes in Confined, Rotating Environments

Christopher J. Howland

Sep 2018

Bib PDF

@techreport{howland_turbulent_2018-1,
  title = {Turbulent Point Source Plumes in Confined, Rotating Environments},
  author = {Howland, Christopher J.},
  year = {2018},
  month = sep,
  institution = {{Woods Hole Oceanographic Institution}},
}

2016

It’s Harder to Splash on Soft Solids

Christopher J. Howland, Arnaud Antkowiak, J. Rafael Castrejón-Pita, and 4 more authors

Phys. Rev. Lett., Oct 2016

Abs DOI Bib

Droplets splash when they impact dry, flat substrates above a critical velocity that depends on parameters such as droplet size, viscosity, and air pressure. By imaging ethanol drops impacting silicone gels of different stiffnesses, we show that substrate stiffness also affects the splashing threshold. Splashing is reduced or even eliminated: droplets on the softest substrates need over 70% more kinetic energy to splash than they do on rigid substrates. We show that this is due to energy losses caused by deformations of soft substrates during the first few microseconds of impact. We find that solids with Young’s moduli \( ≲100  \textrm{kPa} \) reduce splashing, in agreement with simple scaling arguments. Thus, materials like soft gels and elastomers can be used as simple coatings for effective splash prevention. Soft substrates also serve as a useful system for testing splash-formation theories and sheet-ejection mechanisms, as they allow the characteristics of ejection sheets to be controlled independently of the bulk impact dynamics of droplets.
@article{howland_its_2016, title = {It's {{Harder}} to {{Splash}} on {{Soft Solids}}}, author = {Howland, Christopher J. and Antkowiak, Arnaud and {Castrej{\'o}n-Pita}, J. Rafael and Howison, Sam D. and Oliver, James M. and Style, Robert W. and {Castrej{\'o}n-Pita}, Alfonso A.}, year = {2016}, month = oct, journal = {Phys. Rev. Lett.}, volume = {117}, number = {18}, pages = {184502}, doi = {10.1103/PhysRevLett.117.184502}, }

Modelling Turbulent Flow Using Large Eddy Simulation

Christopher J. Howland

Oct 2016

Bib PDF

@phdthesis{howland_modelling_2016-1,
  type = {Masters Dissertation},
  title = {Modelling {{Turbulent Flow Using Large Eddy Simulation}}},
  author = {Howland, Christopher J.},
  year = {2016},
  school = {University of Oxford},
}